La elipse.
Definición de elipse: la elipse es el lugar geométrico de los puntos del plano \(P(x,\ y)\) cuya suma de las distancias a dos puntos fijos llamados focos es constante.
Se excluye el caso de que el punto \(P(x,\ y)\) esté sobre el segmento que une los focos, además está suma es mayor que la distancia entre los focos.
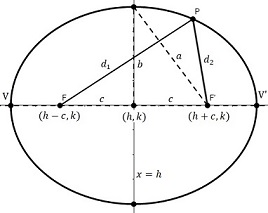
En la figura se muestra una elipse de centro \((h,k)\) cuyos focos \(F\) y \(F'\) son los puntos \((h\pm c,k)\). De la definción, a medida que un punto se mueve sobre la elipse \(d_1+d_2=d\) (un valor constante). Para facilitar el análisis algebraico se escoge \(d=2a\).
Los segmentos que van desde el punto \(P\) a los focos son llamados radios vectores y la recta que pasa por los focos recibe el nombre de eje focal. Los puntos \(V\) y \(V'\) son los vértices del eje mayor, los puntos de la intersección de la elipse y la recta \(x=h\) son los vértices del eje menor.
El centro biseca (corta en el punto medio) al segmento \(\overline{FF'}\), la distancia \(2a\) es la longitud del eje mayor, mientras que la distancia \(2b\) es la longitud del eje menor. Note la relación \(a^2=b^2+c^2\) en la figura de arriba.
Algunas utilidades de las elipses en la vida cotidiana.
1. Primera ley de Kepler: esta ley expresa que, todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas con el Sol en uno de sus focos (en el otro foco no hay nada). Este descubrimiento de Johannes Kepler permitió crear un modelo planetario correcto sobre el movimiento de los planetas alrededor del Sol y de otros cuerpos celestes. Kepler tardó dieciséis años en comprender esto, ya que anterior a él, se creía que el dicho movimiento era circular.
2. Al unir cualquier punto, \(P(x,\ y)\) de la elipse con sus focos, el ángulo que forman los radios focales con la tangente en ese punto son iguales.Esta propiedad se utiliza en la construcción de espejos de luz y sonido, pues la emisión, de luz o sonido, desde uno de los focos se refleja en el otro foco.
3. Debido a la resistencia del viento, la cual provoca fuerza de sustentación sobre los aviones, las trayectorias que realizan estos cuando hacen viajes circulares, se vuelven elípticas para aminorar los efectos de esta fuerza.
4. En arquitectura se utilizan con mayor frecuencia arcos con forma elíptica, ya que estos poseen un mejor comportamiento sísmico. Además, existen capillas o galerías de los secretos, las cuales son estructuras con techos elipsoidales que permiten poder oir una persona que está en un foco desde el otro foco y las personas que están entre las otras dos no oirán nada.
5. En la medicina se usa un aparato llamado litotriptor para desintegrar cálculos renales por medio de ondas intra-acuáticas de choque. Éste funciona haciendo que las ondas de choque se generen por medio de un electrodo ubicado dentro de una cámara de agua, estas ondas de choque concentradas por un reflector elíptico que las dirige e impactan en forma directa sobre el cálculo, sin dañar el riñón y así se van fragmentando en determinado tiempo.
6. En muchas ciudades es fácil encontrar plazas de planta elíptica, normalmente conocidas por el nombre de "plaza elíptica". Por ejemplo, en Madrid y Bilbao existen plazas de este tipo. Sin embargo, la plaza de planta elíptica más famosa en el mundo probablemente sea la Plaza de San Pedro en el Vaticano. También se pueden encontrar edificaciones con planta elíptica. Un ejemplo es la iglesia del Monasterio de San Bernardo, más conocido por "Las Bernardas" en Alcalá de Henares. Un templo con una única nave y planta elíptica y cúpula del mismo trazado. En sus muros se abren seis capillas, cuatro de ellas también de planta elíptica, con diferentes tamaños de sus portadas.
Ecuación de la elipse con centro en el punto \((0,0)\).
Considere la elipse de la figura  y suponga que el centro es el punto \(\left(0,0\right)\) esto conlleva a que las coordenadas de los focos son \(\left(-c,0\right)\) y \((c,\ 0)\).
y suponga que el centro es el punto \(\left(0,0\right)\) esto conlleva a que las coordenadas de los focos son \(\left(-c,0\right)\) y \((c,\ 0)\).
De la definición de la elipse la distancia \(d\left(P,F\right)+d\left(P,F^\prime\right)=2a\) de donde se concluye lo siguiente:
\begin{align}
&\sqrt{\left(x+c\right)^2+y^2}+\sqrt{\left(x-c\right)^2+y^2}=2a\\
&\sqrt{\left(x+c\right)^2+y^2}=2a-\sqrt{\left(x-c\right)^2+y^2}\\
&\left(x+c\right)^2+y^2=4a^2-4a\sqrt{\left(x-c\right)^2+y^2}+\left(x-c\right)^2+y^2\\
&\left(x+c\right)^2-\left(x-c\right)^2-4a^2=-4a\sqrt{\left(x-c\right)^2+y^2}\\
&4cx-4a^2=-4a\sqrt{\left(x-c\right)^2+y^2}\\
&cx-a^2=-a\sqrt{\left(x-c\right)^2+y^2}\\
&c^2x^2-2a^2cx+a^4=a^2(\left(x-c\right)^2+y^2)\\
&c^2x^2-2a^2cx+a^4=a^2(x^2-2cx+c^2+y^2)\\
&c^2x^2-2a^2cx+a^4=a^2x^2-2a^2cx+a^2c^2+a^2y^2\\
&c^2x^2+a^4=a^2x^2+a^2c^2+a^2y^2\Longrightarrow a^4-a^2c^2=a^2x^2-c^2x^2+a^2y^2\\
&a^2\left(a^2-c^2\right)=x^2\left(a^2-c^2\right)+a^2y^2
\end{align}
De la relación \(a^2=b^2+c^2\) se tiene \(a^2-c^2=b^2\) de donde la expresión anterior es,
\begin{align}
a^2b^2=x^2b^2+a^2y^2\Longrightarrow\frac{a^2b^2}{a^2b^2}=\frac{x^2b^2}{a^2b^2}+\frac{x^2b^2}{a^2b^2}\\
\end{align}
simplificando y ordenando la expresión se tiene,
Elipse de centro \((0,0)\)
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ~~~~\boxed{\textcolor{#ff0080}{1}}$$ que es la ecuación de una elipse cuyos focos están sobre una recta horizontal y su centro es el origen de coordenadas, para \(a>b\).
Si los focos de la elipse están sobre una recta vertical la ecuación anterior se transforma en, $$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1~~~~\boxed{\textcolor{#ff0080}{2}}$$ de modo que la distancia \(a\) indica la ubicación del eje focal.
Ecuación de la elipse con centro en el punto \(C(h,k)\).
Considere nuevamente la elipse de la figura  ahora centrada en el punto \(C(h,k)\). La recta \(x=h\) representa una traslación horizontal de \(h\) unidades para el eje de ordenada, al igual que la recta \(y=k\) representa una traslación vertical de \(k\) unidades para el eje de abscisa.
ahora centrada en el punto \(C(h,k)\). La recta \(x=h\) representa una traslación horizontal de \(h\) unidades para el eje de ordenada, al igual que la recta \(y=k\) representa una traslación vertical de \(k\) unidades para el eje de abscisa.
Sea el punto \(P'=(x',y')\) entonces la ecuación de la elipse con eje focal horizontal que pasa por él está dada por, $$\frac{{x^\prime}^2}{a^2}+\frac{{y^\prime}^2}{b^2}=1$$ Mediante una traslación definida por un vector \( \vec{V}=(h,k)\) las coordenadas del punto \(P'\) se transforman en \(P'=(x'+h,y'+k)\), escribiendo este punto como \(P=(x,y) \Longrightarrow x-h=x^\prime;\ y-k=y^\prime\) de donde al sustituir estos valores en la ecuación anterior se tiene,
Elipse de centro \((h,k)\)
$$\frac{{(x-h)}^2}{a^2}+\frac{{(y-k)}^2}{b^2}=1$$ que es la ecuación de la elipse con centro en \(C(h,k)\) y eje focal horizontal.
Ecuación general de la elipse.
Si en las ecuaciones de la elipse con centro en el punto \((h,k)\) se realizan las operaciones indicadas e iguala a cero uno de sus miembros, se tiene,
\begin{align}
&\frac{{(x-h)}^2}{a^2}+\frac{{(y-k)}^2}{b^2}=1\\
&b^2{(x-h)}^2+a^2{(y-k)}^2=a^2b^2\\
&b^2\left(x^2-2hx+h^2\right)+a^2\left(y^2-2ky+k^2\right)=a^2b^2\\
&b^2x^2-2b^2hx+b^2h^2+a^2y^2-2a^2ky+a^2k^2=a^2b^2\\
&b^2x^2-2b^2hx+b^2h^2+a^2y^2-2a^2ky+a^2k^2-a^2b^2=0\\
&b^2x^2+a^2y^2-2b^2hx-2a^2ky+b^2h^2+a^2k^2-a^2b^2=0~~~~\boxed{\textcolor{#ff0080}{3}}\\
\end{align}
Ahora llamando a los coeficientes,
\(b^2=A,\) \(a^2=C,\) \(2b^2h=D,\) \(-2a^2k=E,\) \(b^2h^2+a^2k^2-a^2b^2=F\) la ecuación \(\boxed{\textcolor{#ff0080}{3}}\) se escribe como,
Forma general de la elipse
$$Ax^2+Cy^2+Cx+Dy+E=0$$
Consideraciones importante.
Continuando con el estudio teórico de la elipse es necesario comprender que una ecuación de la forma \(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) no siempre representa una elipse, esto es debido a que, según las condiciones dadas, ésta puede representar un punto, una elipse de ejes paralelos a los ejes coordenados o ningún lugar geométrico real en específico.
Si \(b\neq0 en Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) la expresión representa un elipse de ejes rotados. Si \(b=0\) la expresión puede o no representar una elipse, un punto o ningún lugar geométrico, como sigue.
\begin{align}
&Ax^2+Cy^2+Dx+Ey+F=0\\
&\left({Ax}^2+Dx\right)+\left(Cy^2+Ey\right)=F\\
&A\left(x^2+\frac{D}{A}x+\left(\frac{D}{2A}\right)^2\right)+C\left(y^2+\frac{E}{C}y+\left(\frac{E}{2C}\right)^2\right)=-E+{A\left(\frac{D}{2A}\right)}^2+C\left(\frac{E}{2C}\right)^2\\
&{A\left(x+\frac{D}{2A}\right)}^2+C\left(y+\frac{E}{2C}\right)^2=-E+\frac{D^2}{4A}+\frac{E^2}{4C}\\
&\frac{\left(x+\frac{D}{2A}\right)^2}{C}+\frac{\left(y+\frac{E}{2C}\right)^2}{A}=\frac{\frac{D^2}{4A}+\frac{E^2}{4C}-E}{AC}\\
&\frac{\left(x+\frac{C}{2A}\right)^2}{C}+\frac{\left(y+\frac{D}{2B}\right)^2}{A}=\frac{\left(\frac{CD^2+AE^2-4ACE}{4AC}\right)}{AC}\\
&\frac{\left(x+\frac{C}{2A}\right)^2}{C}+\frac{\left(y+\frac{D}{2B}\right)^2}{A}=\frac{CD^2+AE^2-4ACE}{4A^2{AC}^2}
\end{align}
Lo cual produce las siguientes conclusiones para
\(Ax^2+Cy^2+Dx+Ey+F=0\)
1. Si \(CD^2+AE^2-4ACE=0\) la expresion representa un punto único .
2. Si \(CD^2+AE^2-4ACE>0\) la expresión representa una elipse.
3. Si \(CD^2+AE^2-4ACE< 0\) la expresión no representa ningún lugar geométrico real.
Dos propiedades matemáticas importantes de la elipse.
1. Rectas tangente a una elipse
Las ecuaciones de las rectas tangentes de pendientes \(m\) a la elipse \(b^2x^2+a^2y^2=a^2b^2\) están dadas por $$y=mx\pm\sqrt{a^2m^2+b^2}$$ y además la normal a una elipse en cualquiera de sus puntos es bisectriz al ángulo formado por los radios vectores de ese punto.
2. Excentricidad de la elipse
La excentricidad \(\varepsilon\) de una elipse cualquiera se interpreta como un indicador de su forma geométrica, la cual expresa que tan “redondeada o no es la elipse” definida matemáticamente como, $$\varepsilon=\frac{c}{a}$$ Cuanto más cercano a cero es el valor de la excentricidad \(\varepsilon\) más redondeada será la elipse y viceversa, esta es la razón por lo cual la circunferencia es un caso especial de una elipse de excentricidad \(\varepsilon=0\).
Tabla resumen de las propiedades analíticas
$$\begin{array}{l l l l l} ~~~~~~~~~\mathrm{ecuación} & \mathrm{centro} & \mathrm{eje~focal}& \mathrm{~~~focos} & \mathrm{~~Vértices} & \mathrm{vértice}\\ \hline \frac{{(x-h)}^2}{a^2}+\frac{{(y-k)}^2}{b^2}=1 &(h,k) & \mathrm{~~~eje}~~x &(h\pm c,k)&(h\pm a\ ,k) & (h,k\pm b)\\ \hline \frac{{(y-k)}^2}{a^2}+\frac{{(x-h)}^2}{b^2}=1 & (h,k) & \mathrm{~~~eje}~~y &(h,\ k\pm c)&(h,k\pm a)&(h\pm b,k)\\ \hline \mathrm{~~~~~~~~~~donde}& a>b;& a^2=b^2+c^2&~~\varepsilon=c/a\\ \hline \end{array}$$ Note que si el centro de la elipse es el punto \((h,k)=(0,0)\) las ecuaciones anteriores quedan simplificadas a la forma reducida de la ecuación de una elipse
Para ver los ejemplos y luego clic en la pestaña del contenido deseado.
tab-2
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
tab-15
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Una elipse por definición. Determinar la ecuación del lugar geométrico de los puntos \(P\left(x,y\right)\) cuya suma de cuadrados de distancias a los puntos fijos \(A\left(0,0\right)\) y \(B(3,\ -5)\) sea igual a \(20\).
Elipses centradas en el origen.
Ejercicio 1. Dada la ecuación de la elipse $$\frac{x^2}{25}+\frac{y^2}{16}=1$$ determinar las coordenadas de los focos, longitudes del eje mayor y menor, longitud del eje focal y los vértices en ambos ejes y su excentricidad.
Ejercicio 2. Determinar una ecuación de la elipse con centro de centro \(C(0,0)\), si se sabe que la longitud del eje mayor es \(2\sqrt{13}\) y la del eje menor es \(4\), donde su eje focal está sobre el eje de ordenada. Además, escribir las coordenadas de los focos y los vértices.
Eje focal horizontal. Determinar la ecuación de la elipse con centro en el origen, que posee un vértice en el punto \((4,0)\), un extremo del eje menor en \((0,-2)\).
Determinar la ecuación de la elipse con centro en el origen, un vértice en \((6, 0)\) y un foco en \((-1, 0).\)
Eje focal vertical.Determinar la ecuación de la elipse con centro en el origen, un vértice en \((-3, 0)\), un foco en \((0, 2)\)
Analísis total. Para cada una de las siguientes elipses determinar: a) el centro, b) los vértices, c) los extremos del eje menor y d) los focos. \begin{align} &1.~~4x^2+5y^2-24x+20y+36=0\\ &2.~~9x^2+25y^2+18x+150y+9=0\\ \end{align}
Analisis total. Para cada una de las siguientes elipses determinar: a) el centro, b) los vértices, c) los extremos del eje menor y d) los focos. \begin{align} &1.~~9x^2+7y^2-126x-42y+441=0\\ &2.~~4x^2+y^2-16x+2y+13=0 \end{align}
Trabajando con fracciones. Determinar el centro, vertices y los focos de la elipse \(16x^2+36y^2+24x-36y+9=0\)
Determinar la ecuación general de la elipse con centro en el origen, un foco en \((0,7)\) y pasa por el punto \((12,-2)\).
Determinar la ecuación de la elipse con centro en el origen, un foco en \((0,\ 7)\), pasa por \((12,\ -2)\).

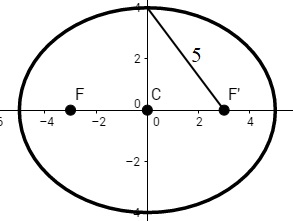 Focos: \(\left(\pm c,0\right)\) entonces \(\left(-3,0\right)\) y \((3,0)\).
Focos: \(\left(\pm c,0\right)\) entonces \(\left(-3,0\right)\) y \((3,0)\).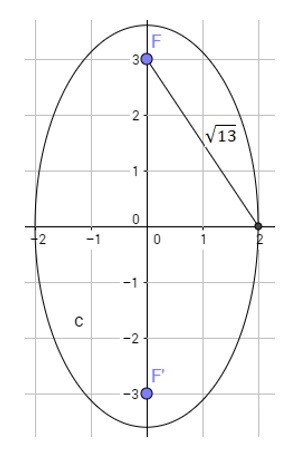
 Solución: dado que el centro es \(C(0,0)\) y un vértice está en \(P(4,0)\) la coordenada en \(x\) de este punto es la distancia del semieje mayor, de donde \(a=4\).
Solución: dado que el centro es \(C(0,0)\) y un vértice está en \(P(4,0)\) la coordenada en \(x\) de este punto es la distancia del semieje mayor, de donde \(a=4\).